|
I can not believe my first year as a pirate is almost over already! I am so thankful for all the support that has made it possible for the math lab to have as many resources and opportunities as it has already have in just the first year! I am blown away with the resources that we have been able to purchase due to the generosity of the PMES community!
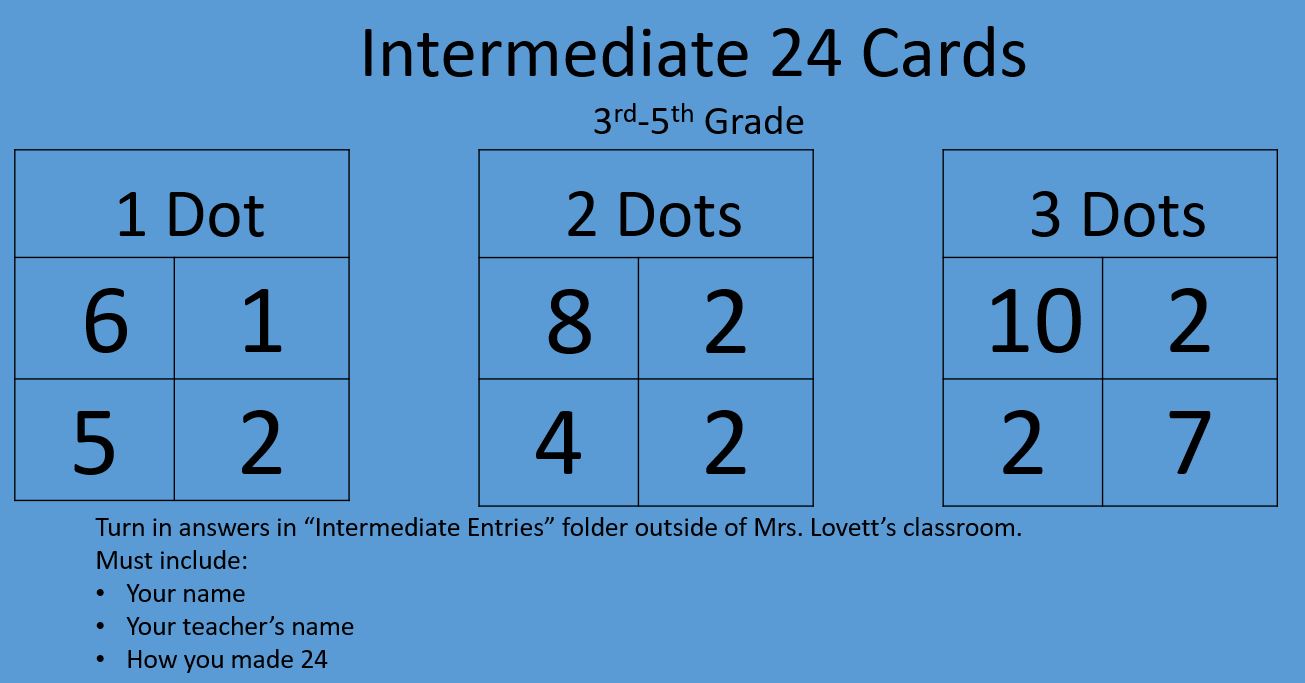
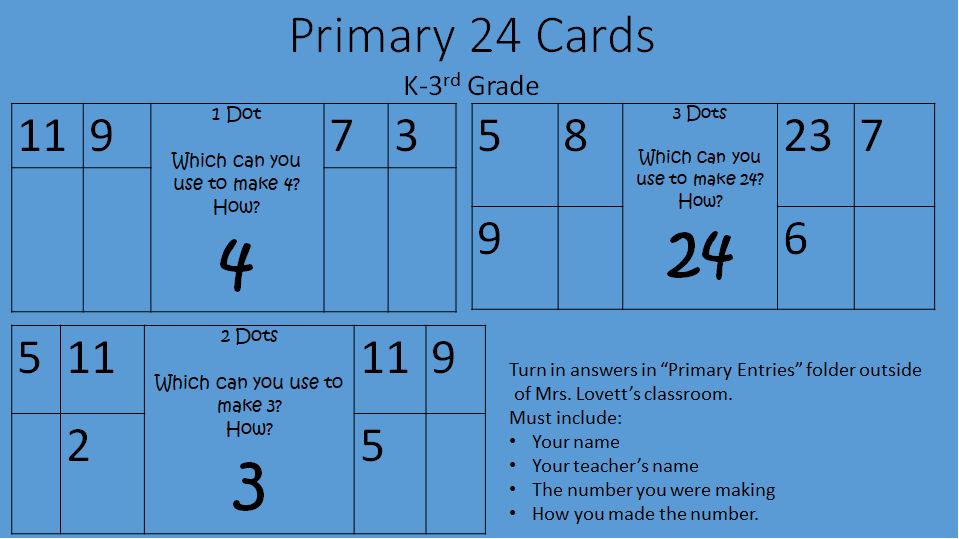
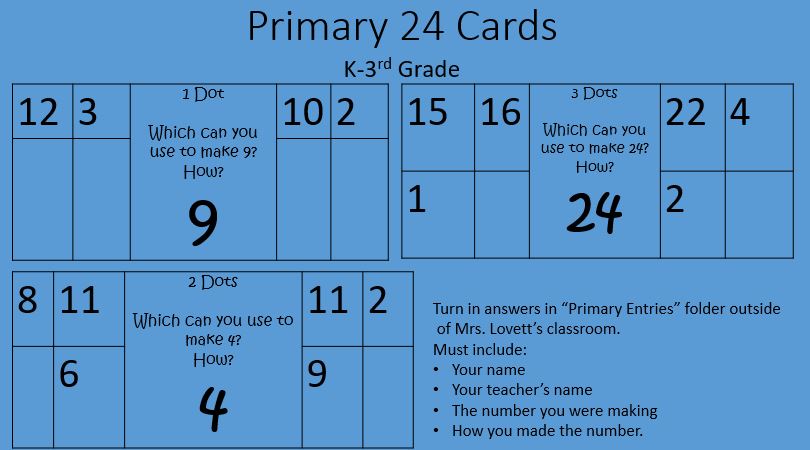
We only have 13 more school days so that means I will only see the students 1-3 more times this year due to all the end of the year fun activities. Here is what we are working on: Kindergarten: Measuring length with various objects and comparing length of different items. 1st Grade: Telling time to the half hour. This is a hard concept for first graders to master! It might be a good one to review this summer. 2nd Grade-5th Grade: We have been playing games, solving mysteries, and escaping rooms to review their grade level content standards. This week we will have our final 24 tournament for the year. |
AuthorMrs. Lovett Archives
June 2019
Categories
All
|








 RSS Feed
RSS Feed
