|
1) Suppose 6 days after the day before yesterday is Thursday. What day of the week is the day after tomorrow?
2) There are 4 separate boxes, and inside each large box there are 3 separate small boxes, and inside each of these small boxes there are 2 separate smaller boxes. How many boxes, counting all sizes, are there altogether? 3) When asked how many gold coins he had, the collector said: If I arrange them in stacks of five, none are left over. If I arrange them in stacks of six, none are left over. If I arrange them in stacks of seven, one is left over. What is the least number of coins he could have? Solutions 1) Make a line-diagram with the following shown on the diagram: N representing now or today, T for tomorrow, and T + 1 for the day after tomorrow, Y for yesterday, and Y - 1 for the day before yesterday. Count 6 days to the right of Y - 1 (the day before yesterday). Mark that day in the diagram as H for Thursday. Count back 2 days to T + 1 (the day after tomorrow). That day is Tuesday. 2) 3) The number of coins must be a multiple of 30. The multiples of 30 are 30, 60, 90, 120, 150, and so on. The smallest of these multiples that leaves a remainder of 1 when divided by 7 is 120.
0 Comments
1) A square is divided into three congruent rectangles as shown below. Each of the three rectangles has a perimeter of 16 meters. How many meters are in the perimeter of the square? 2) A person made a purchase for D dollars and C cents, and gave the cashier a $20 bill. The cashier incorrectly charged the person C dollars and D cents, and returned $4.88 in change. If the cashier had charged the correct price, what would the correct change have been? 3) In the addition problem below, different letters stand for different digits. What five-digit number does SERVE represent? V C R + V C C T S E R V E Solutions 1) Let 3S represent the length of a side of the square as shown in the diagram below. Then the perimeter of one of the congruent rectangles is 8S or 16. It follows that S = 2, and 3S, the length of a side of the square, is 6. Therefore the perimeter of the square is 24 meters. 2) To find the incorrect charge, subtract $4.88 from $20. $20.00 - $ 4.88 incorrect change $15.12 incorrect charge The incorrect charge, $15.12, represents C dollars and D cents. Therefore the correct charge is $12.15. To get the correct change, subtract $12.15 from $20. $20.00 - $12.15 correct charge $ 7.85 correct change 3) Find the values of S, V, and E in that order: S = 1, V = 9, E = 0. Substitute those values in the cryptogram. V C R 9 C R + V C C T + 9 C C T S E R V E 1 0 R 9 0 Clearly R + T in the units column must equal 10 which will yield a carry of 1 in the tens column. So C + C + 1 must end in 9. C can be 9 or 4. But V = 9. So C must be 4. Substitute 4 for C. 9 4 R + 9 4 4 T 1 0 R 9 0 Since there is no carry from the tens column, R in the hundreds column must be 3 (and T in the units column must be 7) SERVE is the number 10390. I can not believe we are almost to the final 9 weeks of the school year. PTA and the Foundation have both been so generous to the Math Lab, I am blown away with all the resources they have gifted us in the first year! I just ordered more games for every grade level and look forward to introducing them to the kids this month. Thank you for all your generosity with all the fundraisers, the money is really enhancing the instruction we are able to do at PMES!
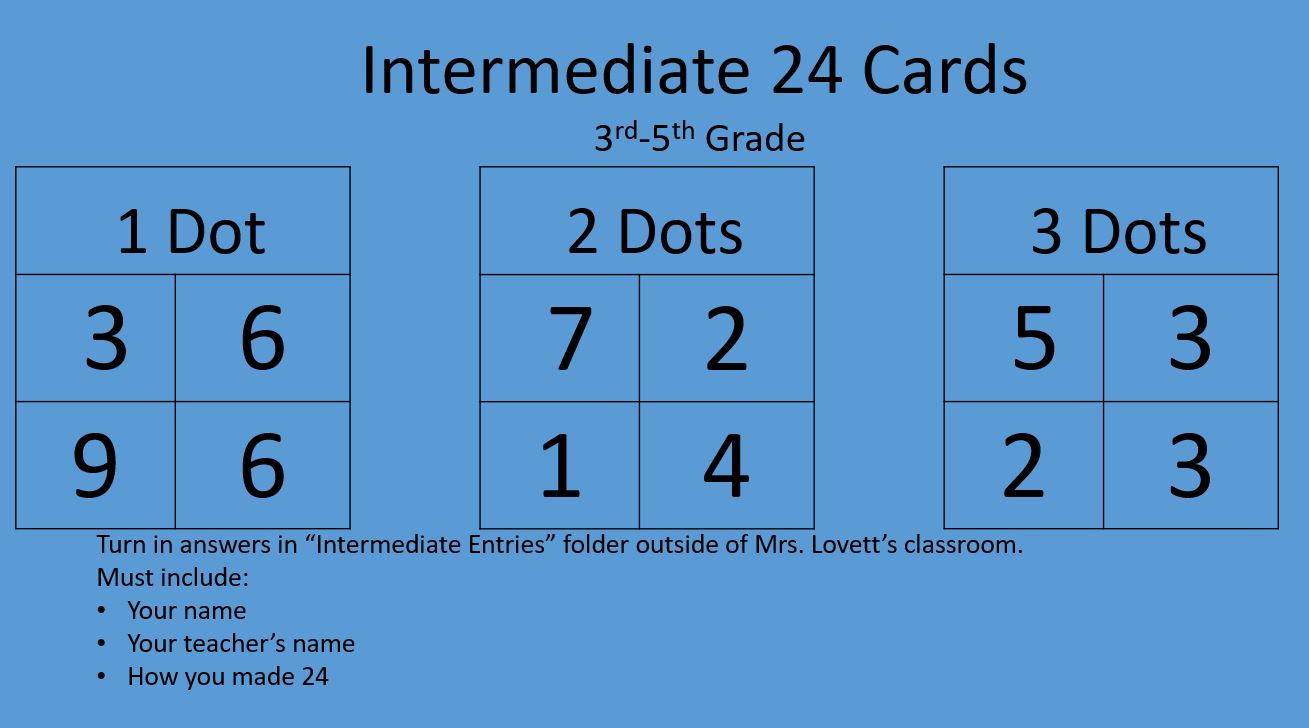
Kindergarten- We will focus on counting on from different numbers and work on addition 1st Grade- Relating addition to subtraction. 2nd Grade- Working on bridging to multiples of 10 in addition 3rd Grade- Using compensation to subtract when the subtrahend has an 8 or 9 in the ones place. 4th Grade- Using building up and building down when multiplying a number with 6 or 9 in the ones place. Test Taking Strategies. 5th Grade- Multi-digit Multiplication. Test Taking Strategies. 2nd-5th graders will be having a 24 tournament the second week in March. 1) Abracadabra has four different coins with values as shown below. Suppose you had just one of each of the four different coins. How many different amounts can be made using one or more of the four different coins?
2) Tom multiplied a number by 2 1/2 and got 50 as an answer. However, he should have divided the number by 2 1/2 to get the correct answer. What is the correct answer? 3) The sum of the ages of Al and Bill is 25; the sum of the ages of Al and Carl is 20; the sum of the ages of Bill and Carl is 31. Who is the oldest of the three and how old is he? Solutions 1) List the possible amounts: 1 coin: produces 1, 2, 4, 8 2 coins: produces 1 + 2, 1 + 4, 1 + 8, 2 + 4, 2 + 8, 4 + 8 3 coins: produces 1 + 2 + 4, 1 + 2 + 8, 1 + 4 + 8, 2 + 4 + 8 4 coins: produces 1 + 2 + 4 + 8 There are 15 different amounts that can be made. Notice that the amounts are the natural numbers from 1 to 15 inclusive. 2) What number multiplied by 2 1/2 gives 50 as an answer? This question is equivalent to finding what number is equal to 50 divided by 2 1/2? That number is 20. To get the correct answer, divide 20 by 2 1/2 producing 8. 3) Method 1 Algebra: Let A, B, and C represent the respective ages of Al, Bill, and Carl. Given (1) A + B = 25 Given (2) A + C = 20 Given (3) B + C = 31 Subtract (2) from (1) (4) B - C = 5 Add (3) and (4) (5) 2B = 36 Divide both sides of (5) by 2 (6) B = 18 From (1) and (2), B is older than C. From (1) and (3), C is older than A. Therefore, Bill is the oldest and he is 18 years old. Method 2 Add conditions (1), (2), and (3) given in Method 1. The sum should be 2A + 2B + 2C = 76. Divide both sides by 2. The result should be (*) A + B + C = 38. Condition (2) states that A + C = 20. Replace A + C in (*) by 20. The result is B + 20 = 38. Clearly B = 18. Therefore Bill is the oldest and he is 18 years old. |
AuthorMrs. Lovett Archives
June 2019
Categories
All
|




 RSS Feed
RSS Feed
