|
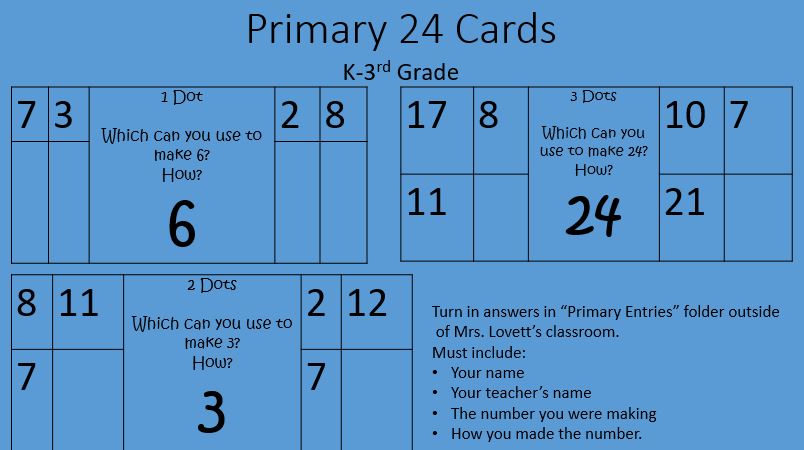
For Primary Cards: Choose the side that you can use the numbers to equal the number in the middle.
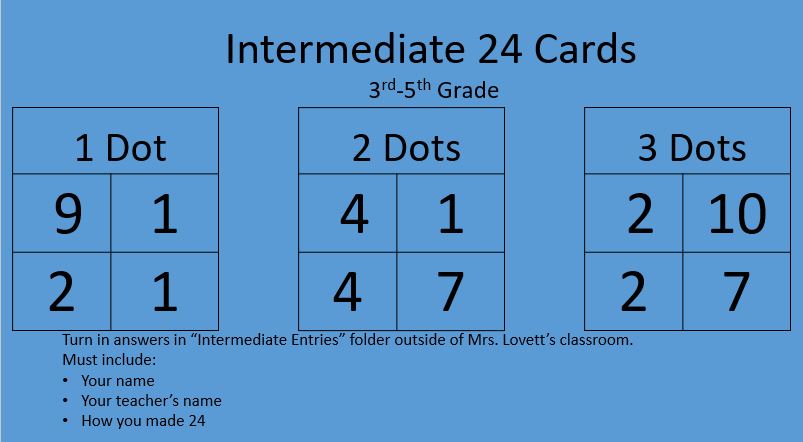
For Intermediate Cards: Make 24 using all 4 numbers once and only once. Turn in your answers for a chance to win a weekly prize
0 Comments
1) A motorist made a 60-mile trip averaging 20 miles per hour. On the return trip, he averaged 30 miles per hour. What was the motorist's average speed for the entire trip?
2) 100 pounds of chocolate is packaged into boxes each containing 1 1/4 pounds of chocolate. Each box is then sold for $1.75. What is the total selling price for all of the boxes of chocolate? 3) In the multiplication problem below, A and B stand for different digits. Find A and B. A B x B A 1 1 4 3 0 4 3 1 5 4 Solutions: 1) The average speed for any trip is the total distance divided by the total time spent in traveling. The total distance was 120 miles and the total time was 5 hours. The average speed equals (120 miles)/(5 hours) or 24 miles/hour or 24 mph. 2) We need to know the number of boxes that were packaged in order to find the total selling price. The number of boxes is obtained by dividing 100 by 1 1/4: 100 divided by 5/4 = 100 x 4/5 = 80. 3) The first partial product 114 is equal to the product of AB and A. The second partial product 304 is equal to the product of AB and B. Then A must be less than B. Method 1: Since the product of AB and A is 114, A is a divisor of 114. Therefore A may be 2, 3, or 6. Since AB x A = 114, A cannot be 2 because AB x A would then be less 60. Similarly, A cannot be 6 since AB x A would then be greater than 360. Therefore A must be 3 and AB must be 114/3 or 38. Thus A = 3 and B = 8. Method 2: From the first partial product, observe that B x A must end in 4. Since A is less than B, A = 2 and B = 7, or A = 3 and B = 8, or A = 4 and B = 6. But 27 x 2 = 54, 46 x 4 = 184, and 38 x 3 = 114. Only the third equation satisfies the given conditions. So A = 3 and B = 8. Method 3: From the second partial product 304, we see that B x B ends in 4. Then B = 2 or 8. If B =2, then A must be 1 because A is less than B. But 12 x 21 = 252. If B = 8 and AB x B = 304, then AB = 304/8 or 38 and 38 x 83 = 3154. Therefore A = 3 and B = 8. it. Primary:
1 Dot: Can you make 4 using 7 and 11 or 6 and 11? How? 2 Dots: Can you make 3 using 8/11/7 or 2/12/7? How? 3 Dots: Can you make 24 using 8/9/21 or 17/14/7? How? Intermediate: 1 Dot: How can you make 24 using 2, 4, 8, and 4? 2 Dots: How can you make 24 using 1, 9, 4, and 7? 3 Dots: How can you make 24 using 2, 3, 5, and 3? 1) Five brothers, each born in a different year, share a gift of $100 according to the following arrangement: each boy, except the youngest, gets $5 more than his next younger brother. How much does the youngest boy get?
2) When I open my math book, two pages face me and the sum of the two page numbers is 317. What is the number of the very next page? 3) 6, 14, and 15 are factors of the natural numbers N. What is the smallest value that N can have? Solutions: 1) Method 1: The average amount received by the 5 boys is $20. In order of age, the third boy receives the average amount of $20. The youngest receives $10 less than the third boy. Therefore, the youngest receives $10. Method 2: Let Y represent the amount received by the youngest boy. Then the amounts received are Y, Y + 5, Y + 10, Y + 15, and Y + 20. These amounts can be regrouped and totaled as Y + Y + Y +Y + Y + 5 + 10 + 15 + 20, or more simply as 5Y + 50. Then, 5Y + 50 = 100, 5Y = 50, and Y = 10. The youngest receives $10. 2) The average of the two consecutive page numbers is 317/2 = 158.5. Then the page numbers are 158 and 159, with 159 being the number of the right-hand page. The next page number is 160. 3) Method 1: The LCM of a set of numbers is the smallest number N which each number of the set will divide exactly. LMC(6,14,15) = 210. Method 2: List the prime factors of each of the given factors of N: 6 = 2 x 3; 14 = 2 x 7, 15 = 3 x 5. N must have 2, 3, 5, and 7 as factors. Then N = 2 x 3 x 5 x 7 = 210. Primary:
1 Dot: Can you make 6 with 6 and 11 or 3 and 9? How? 2 Dots: Can you make 9 with 3/2/4 or 3/10/5? How? 3 Dots: Can you make 24 with 9/2/17 or 8/21/6? How? Intermediate: How can you make 24 with... 1 Dot: 6, 1, 5, 2 2 Dots: 6, 4, 1, 4 3 Dots: 2, 6, 7, 6 The kids love playing Guess My Number, I play it with Kindergarten-Fifth (I just use bigger numbers and they ask different questions according to their age. I found this game where they can mark off the numbers that do not match the clues. www.topmarks.co.uk/learning-to-count/paint-the-squares
Primary:
1 Dot: Can you make 5 with 9 and 4 or 1 and 5? How? 2 Dots: Can you make 5 with 12/3/4 or 10/12/8? How? 3 Dots: Can you make 24 with 9/16/3 or 8/21/11? How? Intermediate: 1 Dot: How can you make 24 using 7, 7, 7, and 3? 2 Dots: How can you make 24 using 5, 6, 8, and 7? 3 Dots: How can you make 24 using 8, 3, 6, and 2? 1) A box contains over 100 marbles. The marbles can be divided into equal shares among 6, 7, or 8 children with 1 marble left over each time. What is the least number of marbles that the box can contain?
2) A fisherman sold some big fish at $4 each and twice as many small fish at $1 each. He received a total of $72 for the big and small fish. How many big fish did he sell? 3) In the addition example below, different letters represent different digits. What digit does A represent? A A + A A C A B Solutions: 1) Use a simpler problem. Instead of one marble being left over each time, assume that no marbles were left over each time. Then the least number of marbles is the LCM(6, 7, 8) which is equal to 3 x 7 x 8 = 168. However, since one marble should be left over each time, the least number of marbles in the box is 168 + 1 = 169. 2) For each big fish sold for $4, two small fish were sold for $1 each. One big fish and two small fish were sold for a total of $6. Since the total received for big and little fish was $72, there were 72/6 = 12 sets of 1 big fish and 2 little fish sold. Therefore 12 big fish were sold. 3) Method 1: A has to be 5 or more. Otherwise the sum will not be a three-digit number. In the second column, A + A + 1 ends in A. Then A is odd, so A = 5, 7, or 9. The only value that checks is 9. Therefore A is 9. Method 2: Use expanded notation: AA = 10A + A = 11A. Then AA + AA = 22A. Therefore C must be 1 and CAB = 100 + 10A + B. Then 22A = 100 + 10A + B. If we subtract 10A from both sides of the equality, the result is 12A = 100 + B. Since 12A has to be greater than 100, A has to be 9. |
AuthorMrs. Lovett Archives
June 2019
Categories
All
|


 RSS Feed
RSS Feed
